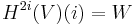Tate conjecture
In mathematics, the Tate conjecture is a 1963 conjecture of John Tate linking algebraic geometry, and more specifically the identification of algebraic cycles, with Galois modules coming from étale cohomology. It is unsolved in the general case, as of 2010[update], and, like the Hodge conjecture to which it is related at the level of some important analogies, it is generally taken to be one of the major problems in the field.
Tate's original statement runs as follows. Let V be a smooth algebraic variety over a field k, which is finitely-generated over its prime field. Let G be the absolute Galois group of k. Fix a prime number l. Write H*(V) for the l-adic cohomology (coefficients in the l-adic integers, scalars then extended to the l-adic numbers) of the base extension of V to the given algebraic closure of k; these groups are G-modules. Consider
for the i-fold Tate twist of the cohomology group in degree 2i, for i = 1, 2, ..., d where d is the dimension of V. Under the Galois action, the image of G is a compact subgroup of GL(V), which is an l-adic Lie group. It follows by the l-adic version of Cartan's theorem that as a closed subgroup it is also a Lie subgroup, with corresponding Lie algebra. Tate's conjecture concerns the subspace W ′ of W invariant under this Lie algebra (that is, on which the infinitesimal transformations of the Lie algebra representation act as 0). There is another characterization used for W ′, namely that it consists of vectors w in W that have an open stabilizer in G, or again have a finite orbit.
Then the Tate conjecture states that W ′ is also the subspace of W generated by the cohomology classes of algebraic cycles of codimension i on V.
An immediate application, also given by Tate, takes V as the cartesian product of two abelian varieties, and deduces a conjecture relating the morphisms from one abelian variety to another to intertwining maps for the Tate modules. This is also known as the Tate conjecture, and several results have been proved towards it.
The same paper also contains related conjectures on L-functions.
References
- Tate, John (1965), "Algebraic Cycles and Poles of Zeta Functions", in Schilling, O. F. G., Arithmetical Algebraic Geometry, New York: Harper and Row.